Matriz de referência de Matemática - Paraná

9º ano do Ensino Fundamental

I. Números e álgebra

Descritor 11 - Determinar a solução de um sistema de equações do 1° grau.

Item de acordo com a Matriz de Referência:

(M090470B1) Resolva o sistema abaixo.

abre chave, primeira equação: 2x mais y igual a 5, segunda equação: x mais 2y igual a 1

A solução desse sistema é

x = 3 e y = 1.
x = 3 e y = -1.
x = 1 e y = 3.
x = -3 e y = 1.

Resposta

GABARITO - B

A habilidade avaliada neste item é a de resolver um sistema de duas equações do primeiro grau. O sistema 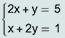abre chave, primeira equação: 2x mais y igual a 5, segunda equação: x mais 2y igual a 1 pode ser resolvido pelo método da substituição. Para isso, isola-se y na primeira equação, obtendo-se y = 5- 2x. Substituindo essa expressão de y na segunda equação, esta fica x + 2(5 - 2x) = 1, ou seja, -3x = -9, cuja solução é x = 3. Voltando com esse valor de x na equação y = 5 - 2x, resulta y = -1. Portanto, a solução do sistema é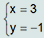 abre chave, primeira equação: x igual a 3, segunda equação: x igual a -1

A alternativa A foi a mais procurada, sendo escolhida por 29,8% dos estudantes. Eles encontraram o valor correto x = 3, mas provavelmente erraram em alguma conta, ou omitem o sinal negativo, dando como resposta y = 1, ao invés de y = -1 .

A alternativa B a correta, foi escolhida por 29,4% dos estudantes, que têm a habilidade avaliada pelo item.

A alternativa C foi escolhida por 27,7% dos estudantes, e a D por 12,6% dos estudantes, que erraram tanto o valor de x como o de y. Eles, provavelmente, ou não fizeram corretamente as substituições ou erraram em alguma conta.